12音から7音選ぶ場合の数は66通りあります。（回転して同じになるものを除く）
そのうち対称なものは10通りあるので実質38種類です。（(66-10)÷2+10）
この辺の説明とか表記とかはここを参照

スケールの型名について雑な説明
・αβγ…ηは「ファドソレラミシ」(♯がつく順番)・「シミラレソドファ」(♭がつく順番)に対応します。
・同じ形のスケールの内、♯♭一方のみでその数が最も少ないものを選んで、♯か♭がつく音をαβ…で表します。（例：2♯ → δ）
・非対称なスケールの場合、上で選んだものが♯か♭かを±として後ろにつけます。
（例：5だけが♯のスケール→「γ+」、3と5だけが♭のスケール→「βε-」）

型名の変換
・β→αの向きを「手前」、α→βの向きを「奥」と表現することにします。異符号側では逆になります。
・手前側に型名をずらす場合
　・αがある → αを消してそれ以外を手前にずらす
　・αがない → 異符号側にαを追加してそれ以外を手前にずらす
・全て異符号側にずらす操作を「反転」と表現しています。例えばεまである型名の場合5回手前側にずらす操作と同じです。（εが5番目なので）
　・型名にあるかないか（例：βε+ → ×○××○）
　・奥側から読んでいって×と○を入れ替える（逆から読んで○××○× → ×○○×○）
　・これを文字に直して異符号にする（×○○×○ → βγε-）

---

型名の一番最後の記号で分類します。例：γδ→最後がδなので「δ系スケール」

13種類に分類できます。

---

ここを参照

---

ここで考えた制限(3度・4度の幅)をなくして他の色んなスケールも考えてみます。
候補が多すぎるのでεを含むスケールを考えることにします。
εまでに拡大すると4組8個のスケールが追加されます。

• ε+(6♯など)・ε-(5♭など)
• βε+(16♯など)・βε-(35♭など)
• γε+(56♯など)・γε-(65♭など)
• δε+(26♯など)・δε-(25♭など)

---

ζがある場合はαも追加しないと音が重なってしまいます。
αがあるのでζ系スケールっぽいものはε以下のスケールと同じになります。
型名にζが含まれるスケールはないということになります。

ηがある場合はβも追加する必要があります。ζもある場合αβがあることになるのでε以下のスケールになります。
η系スケールまで拡大すると4組8個のスケールが追加されます。

• βη+(17♯など)・βη-(34♭など)
• βγη+(157♯など)・βγη-(346♭など)
• βδη+(127♯など)・βδη-(234♭など)
• βεη+(167♯など)・βεη-(345♭など)

---

ダブルシャープ・ダブルフラットがつくものは後ろに²をつけることにします。
α²スケールの場合、αがあるのでη以下のスケールと同じになります。（同じ形のスケールを考える時は「αβ…ηα」のように後ろに繋げていく）
型名にα²が含まれるスケールはないということになります。

β²がある場合はδも追加する必要があります。

何を追加する必要があるのかわかりやすくするために番号を振ってみます。

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
α	β	γ	δ	ε	ζ	η	α²	β²	γ²	δ²	ε²	ζ²	η²	α‪³‬
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
β‪³‬	γ‪³‬	δ‪³‬	ε‪³‬	ζ‪³‬	η‪³‬	α⁴	β⁴	γ⁴	δ⁴	ε⁴	ζ⁴	η⁴	α⁵	β⁵

基本型名に存在し得ない(αは例外)ものをグレーに塗りました。
・5で割った余りが1のもの
・8以降で余り3のもの
・15以降で余り0のもの
・22以降で余り2のもの
・29以降で余り4のもの
がグレーになっています。

それぞれが型名に存在するために必要な条件は
・-5nがすべて存在する
・-8nがすべて存在する
となります。

上の条件を満たして、文字数(γ3などはその数カウント)がnの半分以下となるものを探します。
nのちょうど半分 かつ 反転しても同じ形になる場合は対称なスケールです。

例：ε²(12)の場合

α	β	γ	δ	ε	ζ	η	α²	β²	γ²	δ²	ε²
×	●	○	○	●	×	●	×	δ	γ	×	●

●：必須　○：自由　×：不可　それ以外：その文字があれば○

必須のβε²ηに合計6文字以内になるように足していく感じで
1つ足す→ γ、δ
2つ足す→ γとδ、γとγ²、δとβ²

βγδε²ηは対称（×○○○○×○ ××××○） ※βγ²ε²ηとβ²δε²ηは反転すると同じ（この場合のみ）（辞書順でβγ²ε²ηを採用）
（×○○×○×○ ××○×○ ⇔ ×○×○○×○ ×○××○）

---

上のように求めるとこうなります。
※[記号](±) → [記号]+と[記号]-

n	分類	型	個数	累計
1	α	α	1	1
2	β	β	1	2
3	γ	γ(±)	2	4
4	δ	δ(±), βδ, γδ	4	8
5	ε	ε(±), βε(±), γε(±), δε(±)	8	16
7	η	βη(±), βγη(±), βδη(±), βεη(±)	8	24
9	β²	β²δ(±), β²γδ(±), β²δε(±), β²δη(±)	8	32
10	γ²	γ²ε(±), βγ²ε(±), γ²δε(±), βγ²δε, βγ²εη	8	40
12	ε²	βε²η(±), βγε²η(±), βδε²η(±), βγδε²η, βγ²ε²η(±)（=β²δε²η(∓)）	9	49
14	η²	β²δη²(±), β²γδη²(±), β²δεη²(±), β²γδεη², β²δε²η²	8	57
17	γ‪³‬	βγ‪³‬ε²η(±), βγ‪³‬δε‪²η(±)	4	61
19	ε‪³‬	β²δε‪³η²(±), β²γδε‪³‬η²(±)‬	4	65
24	γ⁴	β²γ⁴δε‪³‬η²	1	66

---

どの2度の音程が何個含まれているかで分類できます。
12個の音のうちスケールに含まれない音は5個なので、
(1,1,1,1,1), (2,1,1,1), (2,2,1), (3,1,1), (3,2), (4,1), (5)の7通りに分けられます。

分類	型	個数	累計
(11111)	α, β, βδ	3	3
(2111)	γ(±), δ(±), ε(±), βε(±), γε(±), βη(±), βδη(±), βεη(±), β²δ(±), β²δη(±)	20	23
(221)	γδ, δε(±), βγη(±), β²γδ(±), β²δε(±), βγε²η(±), βγδε²η, β²δεη²(±), β²γδεη²	15	38
(311)	γ²ε(±), βγ²ε(±), βγ²δε, βγ²εη, βε²η(±), βδε²η(±), βγ²ε²η(±), β²δη²(±), β²δε²η²	15	53
(32)	γ²δε(±), β²γδη²(±), β²γδε‪³‬η²(±)	6	59
(41)	βγ‪³‬ε²η(±), βγ‪³δ‬ε²η(±), β²δε‪³‬η²(±)	6	65
(5)	β²γ⁴δε‪³‬η²	1	66

---

半音の塊(3音連続半音など)で分けることもできます。
使われる7音の分割の仕方で、使われない音が5個しかないことを考慮すると
(2,2,1,1,1), (2,2,2,1), (3,1,1,1,1), (3,2,1,1), (3,2,2), (3,3,1), (4,1,1,1), (4,2,1), (4,3), (5,1,1), (5,2), (6,1), (7)の13通りに分けられます。

分類	型	個数	累計
(22111)	α, β	2	2
(2221)	γ(±), βε(±)	4	6
(31111)	βδ	1	7
(3211)	δ(±), ε(±), γε(±), βη(±), βδη(±), βεη(±)	12	19
(322)	γδ, βγη(±), βγ²ε(±), βγ²εη	6	25
(331)	δε(±), βγ²δε, βδε²η(±), βγδε²η	6	31
(4111)	β²δ(±), β²δη(±)	4	35
(421)	β²γδ(±), β²δε(±), γ²ε(±), βε²η(±), βγε²η(±), βγ²ε²η(±)	12	47
(43)	γ²δε(±), βγ‪³‬δε²η(±)	4	51
(511)	β²δη²(±), β²δεη²(±), β²γδεη², β²δε²η²	6	57
(52)	β²γδη²(±), βγ‪³‬ε²η(±)	4	61
(61)	β²δε‪³‬η²(±), βγδε‪³‬η²(±)	4	65
(7)	β²γ⁴δε‪³‬η²	1	66

---

音程と半音の分類の組み合わせは、分割する数は同じになるので

• (11111) - (22111)or(31111)
• (2111) - (2221)or(3211)or(4111)
• (221)or(311) - (322)or(331)or(421)or(511)
• (32)or(41) - (43)or(52)or(61)
• (5) - (7)

の2+3+8+6+1=20通りになります。

片方が1通りしかないものは上の表でわかるので3分割・2分割のものだけ示します。
66個中42個が当てはまります。

分類	型	個数
(221)-(322)	γδ, βγη(±)	3
(221)-(331)	δε(±), βγδε²η	3
(221)-(421)	β²γδ(±), β²δε(±), βγε²η(±)	6
(221)-(511)	β²δεη²(±), β²γδεη²	3
(311)-(322)	βγ²ε(±), βγ²εη	3
(311)-(331)	βγ²δε, βδε‪²η(±)	3
(311)-(421)	γ²ε(±), βε²η(±), βγ²ε²η(±)	6
(311)-(511)	β²δη²(±), β²δε²η²	3
(32)-(43)	γ²δε(±)	2
(32)-(52)	β²γδη²(±)	2
(32)-(61)	β²γδε‪³‬η²(±)	2
(41)-(43)	βγ‪³‬δε²η(±)	2
(41)-(52)	βγ‪³‬ε²η(±)	2
(41)-(61)	β²δε‪³‬η²(±)	2

---

番号が2つあるのは+が最初の数字、-が後ろの数字
型②：♯♭の和が0になるようにした型名 or ×か♭♭が残ってなくせる場合はなくなるまでずらした型名
（求め方：αからn個は反転、それより後ろはn個α側にずらす）
対：対称なスケール

系	番号	型①	型②	対	音程	半音
α	1-1	α		○	(11111)	(22111)
β	2-1	β	α±	○	(11111)	(22111)
γ	3-1,2	γ(±)	α-β+(±)		(2111)	(2221)
δ	4-1,2	δ(±)	α-γ+(±)		(2111)	(3211)
	4-3	βδ	β±	○	(11111)	(31111)
	4-4	γδ	α±β±	○	(221)	(322)
ε	5-1,2	ε(±)	α-δ+(±)		(2111)	(3211)
	5-3,4	βε(±)	β-γ+(±)		(2111)	(2221)
	5-5,6	γε(±)	α±β-γ+(±)		(2111)	(3211)
	5-7,8	δε(±)	α-β±γ+(±)		(221)	(331)
η	7-1,2	βη(±)	β-ε+(±)		(2111)	(3211)
	7-3,4	βγη(±)	γ-δ+(±)		(221)	(322)
	7-5,6	βδη(±)	α±γ-δ+(±)		(2111)	(3211)
	7-7,8	βεη(±)	α-β+γ-δ+(±)		(2111)	(3211)
β²	9-1,2	β²δ(±)	α±γ-ζ+(±)		(2111)	(4111)
	9-3,4	β²γδ(±)	δ-ε+(±)		(221)	(421)
	9-5,6	β²δε(±)	α+β-δ-ε+(±)		(221)	(421)
	9-7,8	β²δη(±)	β-γ+δ-ε+(±)		(2111)	(4111)
γ²	10-1,2	γ²ε(±)	β±γ-η+(±)		(311)	(421)
	10-3,4	βγ²ε(±)	α±δ-ζ+(±)		(311)	(322)
	10-5,6	γ²δε(±)	α+γ-δ-ζ+(±)		(32)	(43)
	10-7	βγ²δε	ε±	○	(311)	(331)
	10-8	βγ²εη	β±ε±	○	(311)	(322)
ε²	12-1,2	βε²η(±)	β±γ-ε-η+(±)		(311)	(421)
	12-3,4	βγε²η(±)	β±ε-η+(±)		(221)	(421)
	12-5,6	βδε²η(±)	β+γ-ε-η+(±)		(311)	(331)
	12-7	βγδε²η	α±ζ±	○	(221)	(331)
	12-8,9	βγ²ε²η(±)※	α±γ-δ+ζ±(±)		(311)	(421)
η²	14-1,2	β²δη²(±)	β±γ-ε-η±(±)		(311)	(511)
	14-3,4	β²γδη²(±)	β±γ-η±(±)		(32)	(52)
	14-5,6	β²δεη²(±)	β±ε-η±(±)		(221)	(511)
	14-7	β²γδεη²	β±η±	○	(221)	(511)
	14-8	β²δε²η²	β±ε±η±	○	(311)	(511)
γ‪³‬	17-1,2	βγ‪³‬ε²η(±)	β-γ²+δ-ε+η-(±)		(41)	(52)
	17-3,4	βγ‪³‬δε²η(±)	α²-β²+γ-δ+(±)		(41)	(43)
ε‪³‬	19-1,2	β²δε‪³‬η²(±)	α+α²-γ-δ²+ζ±(±)		(41)	(61)
	19-3,4	β²γδε‪³‬η²(±)	β²-γ²+δ-ε+(±)		(32)	(61)
γ⁴	24-1	β²γ⁴δε‪³‬η²	β±ε²±η±	○	(5)	(7)

※β²δε²η(∓)も同じ

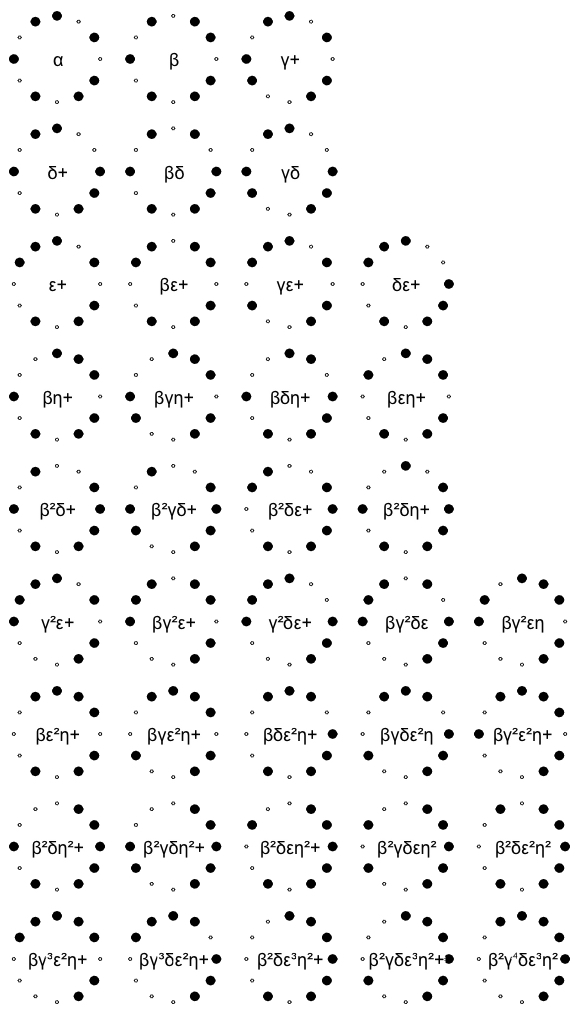
※12時の点から時計回りにドレミファソラシドで配置してるけど回したりしても一緒
※非対称なのは+のほうだけ表示（-は反転すれば作れる）
※対称なのは+のほうを元に配置

音が偏りすぎているものは使う機会がほとんどないと思います。
上の表では 2度が増2度以内・半音の連続3つ以内 になるものを分類別に色をつけました。

2度・3度・5度の幅
赤：上から見ていって新しく使えるようになるもの
青：周りより幅が狭いもの
※(略)＜増＜重増＜三重増＜四重増

系	番号	型	2度	3度	5度
α	1-1	α	短〜長	短〜長	減〜完全
β	2-1	β	短〜長	短〜長	減〜増
γ	3-1,2	γ(±)	短〜増	短〜長	減〜増
δ	4-1,2	δ(±)	短〜増	減〜長	減〜増
	4-3	βδ	短〜長	減〜長	減〜増
	4-4	γδ	短〜増	減〜長	減〜増
ε	5-1,2	ε(±)	短〜増	減〜増	減〜増
	5-3,4	βε(±)	短〜増	短〜増	減〜増
	5-5,6	γε(±)	短〜増	減〜増	減〜増
	5-7,8	δε(±)	短〜増	減〜増	減〜増
η	7-1,2	βη(±)	短〜増	減〜増	重減〜増
	7-3,4	βγη(±)	短〜増	減〜長	重減〜増
	7-5,6	βδη(±)	短〜増	減〜増	重減〜増
	7-7,8	βεη(±)	短〜増	減〜増	重減〜増
β²	9-1,2	β²δ(±)	短〜増	減〜増	重減〜重増
	9-3,4	β²γδ(±)	短〜増	減〜増	減〜重増
	9-5,6	β²δε(±)	短〜増	減〜増	重減〜重増
	9-7,8	β²δη(±)	短〜増	減〜増	重減〜重増
γ²	10-1,2	γ²ε(±)	短〜重増	減〜増	重減〜重増
	10-3,4	βγ²ε(±)	短〜重増	減〜増	重減〜増
	10-5,6	γ²δε(±)	短〜重増	減〜増	減〜重増
	10-7	βγ²δε	短〜重増	減〜増	減〜増
	10-8	βγ²εη	短〜重増	減〜増	重減〜増
ε²	12-1,2	βε²η(±)	短〜重増	減〜重増	重減〜重増
	12-3,4	βγε²η(±)	短〜増	減〜重増	重減〜重増
	12-5,6	βδε²η(±)	短〜重増	減〜重増	重減〜増
	12-7	βγδε²η	短〜増	減〜重増	重減〜増
	12-8,9	βγ²ε²η(±)	短〜重増	減〜重増	重減〜重増
η²	14-1,2	β²δη²(±)	短〜重増	減〜重増	三重減〜重増
	14-3,4	β²γδη²(±)	短〜重増	減〜増	三重減〜重増
	14-5,6	β²δεη²(±)	短〜増	減〜重増	三重減〜重増
	14-7	β²γδεη²	短〜増	減〜増	三重減〜重増
	14-8	β²δε²η²	短〜重増	減〜重増	三重減〜重増
γ‪³‬	17-1,2	βγ‪³‬ε²η(±)	短〜三重増	減〜重増	三重減〜重増
	17-3,4	βγ‪³‬δε²η(±)	短〜三重増	減〜重増	重減〜重増
ε‪³‬	19-1,2	β²δε‪³‬η²(±)	短〜三重増	減〜三重増	三重減〜重増
	19-3,4	β²γδε‪³‬η²(±)	短〜重増	減〜三重増	三重減〜重増
γ⁴	24-1	β²γ⁴δε‪³‬η²	短〜四重増	減〜三重増	三重減〜重増

短,長2度・短,長3度・減,完全5度（α）
→増5度（β）→増2度（γ）
→減3度（δ）→増3度（ε）
→重減5度（η）→重増5度（β²）
→重増2度（γ²）→重増3度（ε²）
→三重減5度（η²）→三重増2度（γ‪³‬）
→三重増3度（ε‪³‬）→四重増2度（γ⁴）

αがないので4(♯)か7(♭)は固定
β：5度+（♯：4〜1、♭：3〜7）
γ：2度+（♯：4〜5、♭：6〜7）
δ：3度-（♯：2〜4、♭：7〜2）
ε：3度+（♯：4〜6、♭：5〜7）
ζ：2度-（♯：3〜6、♭：7〜1）
η：5度-（♯：7〜4、♭：7〜4）

その系で初めて使えるようになった音程はその系全ての型で使える

♯♭和は0

	4♯	1♯	5♯	2♯	6♯
7♭	β	γ+	δ+	ε+	ζ+
3♭	γ-	βδ	βε+	βζ+	βη+
6♭	δ-	βε-	βγζ	βγη+
2♭	ε-	βζ-	βγη-		β²γδ+
5♭	ζ-	βη-		β²γδ-	βγ²δε

• 小さい方がα → 大きい方+1
• 小さい方がβ → βと大きい方+2
• 小さい方がγ → βγと大きい方+3
• 小さい方がδ → βγδと大きい方+4

---

αがあると調性が曖昧になるのでそれを含まないスケールが基準っぽくなる説

条件：αとηがない

• αがない（♯だけor♭だけの場合(各1個まで)、混在する場合）
• ♯だけ♭だけ → 型名そのままの形とそれを反転した形
• 混在するパターンの数 → 隙間の数（β²δε+の場合：βとδε、δεとβ²の間が空いているので2個）
• → 隙間の端で反転させた形（β以下を反転→β±γ+η+, ε以下を反転→γ-δ+ε-）

(±)は略
β/γε → β-γ+ε+とβ+γ-ε-

系	番号	型	♯♭片方	♯♭混在
α	1-1	α	(0)
β	2-1	β	β
γ	3-1,2	γ(±)	γ, βγ
δ	4-1,2	δ(±)	δ, βγδ
	4-3	βδ	βδ	β/β
	4-4	γδ	γδ
ε	5-1,2	ε(±)	ε, βγδε
	5-3,4	βε(±)	βε, βγε	β/γ
	5-5,6	γε(±)	γε, βδε	βγ/β
	5-7,8	δε(±)	δε, γδε
η	7-1,2	βη(±)	(βη, βγδεη)	β/ε
	7-3,4	βγη(±)	(βγη, βγδη)	γ/δ
	7-5,6	βδη(±)	(βδη, βγεη)	β/βε, βδ/γ
	7-7,8	βεη(±)	(βεη, βδεη)	β/γε, βγε/β
β²	9-1,2	β²δ(±)	β²δ, (β²γδεη)	(β/βη), βδ/ε
	9-3,4	β²γδ(±)	β²γδ, β²γδε	δ/ε
	9-5,6	β²δε(±)	β²δε, (β²γδη)	(β/βγη), γε/δ
	9-7,8	β²δη(±)	β²δη, (β²δεη)	(β/βεη), βδ/γε, (βγεη/β)
γ²	10-1,2	γ²ε(±)	γ²ε, (β²γ²δεη)	(βγ/βη), βδε/ε
	10-3,4	βγ²ε(±)	βγ²ε, (βγ²δεη)	(γ/βη), βε/ε
	10-5,6	γ²δε(±)	γ²δε, β²γ²δε	δε/ε
	10-7	βγ²δε	βγ²δε	ε/ε
	10-8	βγ²εη	(βγ²εη)	(γ/βδη), βε/βε
ε²	12-1,2	βε²η(±)	(βε²η, β²γ²δε²η)	β/γ²ε, (βγε/βη), (βδεη/ε)
	12-3,4	βγε²η(±)	(βγε²η, β²γδε²η)	γ/β²δ, (βε/βη), (βδη/ε)
	12-5,6	βδε²η(±)	(βδε²η, βγ²δε²η)	β/βγ²ε, (γε/βη), (βεη/ε)
	12-7	βγδε²η	(βγδε²η)	(ε/βη)
	12-8,9	βγ²ε²η(±)	(βγ²ε²η, β²δε²η)	(γ/β²δη), (βε/βεη), (βδη/γε), (βγ²εη/β)
η²	14-1,2	β²δη²(±)
	14-3,4	β²γδη²(±)
	14-5,6	β²δεη²(±)
	14-7	β²γδεη²
	14-8	β²δε²η²
γ‪³‬	17-1,2	βγ‪³‬ε²η(±)
	17-3,4	βγ‪³‬δε²η(±)
ε‪³‬	19-1,2	β²δε‪³‬η²(±)
	19-3,4	β²γδε‪³‬η²(±)
γ⁴	24-1	β²γ⁴δε‪³‬η²

←前へ一覧へ 次へ→