• 時間は0→1（t = obj.time/(obj.totaltime+1/30)とかして扱う）（周期関数除く）
• 値は0→1（f(t)に動かしたい分だけかける）
• 速度は移動幅(0→1で移動させる幅)に比例、移動時間(t=0→1の時間)に反比例
• 加速度は移動幅に比例、移動時間の2乗に反比例

---

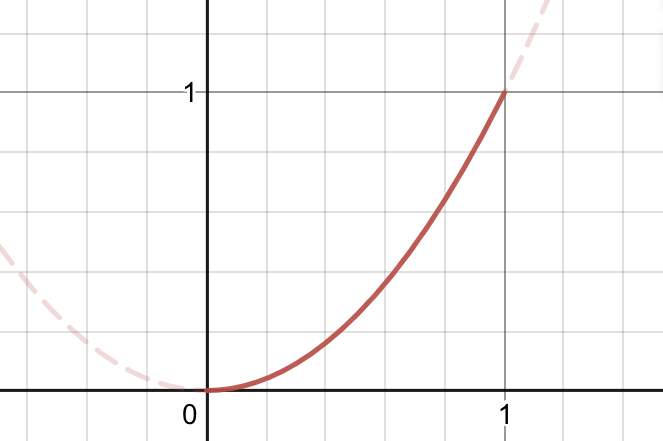\[f(t) = t^2\]

コピペ用：t^2

• 加速度一定
• 速度0→2

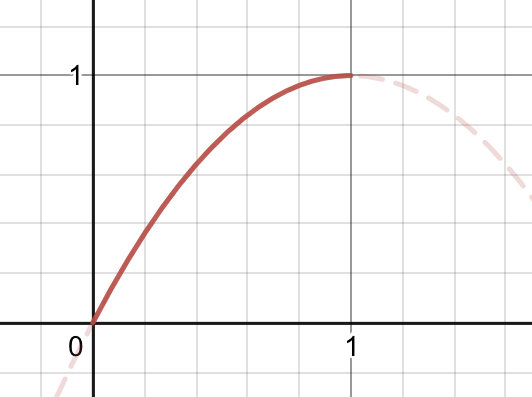\[f(t) = -(t-1)^2+1 = t(2-t)\]

コピペ用：-(t-1)^2+1　t*(2-t)

• 加速度一定
• 速度2→0

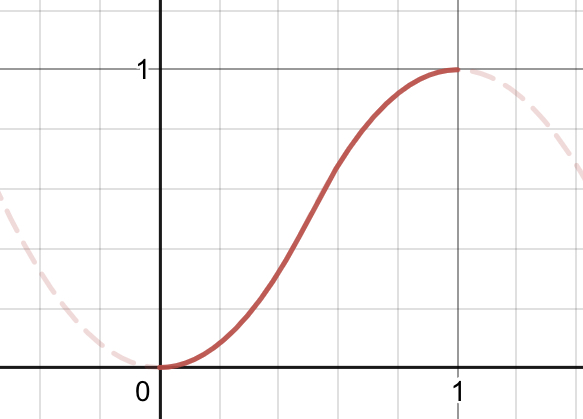\[f(t) = (1-2t)(|t-0.5|-1)+0.5\]

コピペ用：(1-2*t)*(math.abs(t-0.5)-1)+0.5

• t=0.5で加速度が切り替わる
• 速度0→2→0

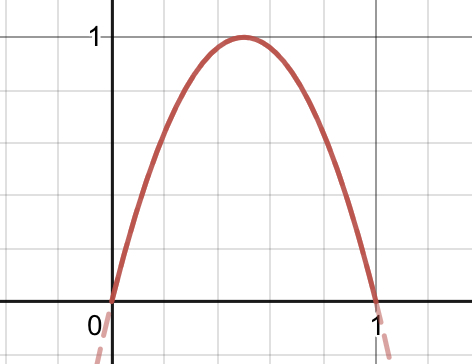\[f(t) = -4(t-0.5)^2+1 = 4t(1-t)\]

コピペ用：-4*(t-0.5)^2+1　4*t*(1-t)

• 加速度一定
• t=0.5で最大f(t)=1
• 速度4→-4

\[f(t) = 4(t\%2-1)(|t\%2-1|-1)\]

コピペ用：4*(t%2-1)*(math.abs(t%2-1)-1)

• f(t)=0のところで加速度が切り替わる
• 周期2
• 振幅1、移動する幅は2
• 速度4→0→-4→0→…

登る場合の概形・関数

\[f(t) = \frac{-(t-p)^2+p^2}{2p-1} = \frac{t(2p-t)}{2p-1}\:(0.5\lt p\lt1)\]

コピペ用：(-(t-p)^2+p^2)/(2*p-1)　t*(2*p-t)/(2*p-1)

• 加速度一定
• pはf(t)が最大になるt
• 0＜p＜0.5にすると「ジャンプして降りる」
• 最大値は\(\frac{p^2}{2p-1}\)

←前へ一覧へ 次へ→